教案是课堂教学的蓝图，是教师对一节课的整体设想。创造性的教学设计，严谨、科学的教学策略将有效提高课堂教学效率，让学生们获得最好的学习效果。以下为安徽敏试教育小编为您整理的教案：小学数学教案《函数的概念》。安徽教师资格网为您提供精彩的教案示范，更多面试资讯欢迎关注敏试教育。

【活动方案】

一、教学目标

1.知识与技能：

了解函数产生的背景，掌握函数的概念、，特别是函数的三要素。会判断什么样的对应

是函数。会求简单函数的定义域及值域。

2.过程与方法：

（1）通过实例，进一步体会函数是描述变量之间的依赖关系的重要数学模型，在此基础上学习用集合与对应的语言来刻画函数，体会对应关系在刻画函数概念中的作用；

（2）了解构成函数的要素；

（3）会求一些简单函数的定义域和值域。

3.情态与价值：使学生感受到学习函数的必要性的重要性，激发学习的积极性。

二、教学重点与难点

重点：理解函数的模型化思想，用集合与对应的语言来刻画函数；

难点：符号“y=f(x)”的含义，函数定义域和值域的区间表示；

三、学法与教学用具

1.学法：学生通过自学、思考、交流、讨论和概括，从而更好地完成本节教学目标 .

2.教学用具：投影仪 .

四、教学思路

（一）创设情景

1.复习初中所学函数的概念，强调函数的模型化思想；

2.阅读课本引例，体会函数是描述客观事物变化规律的数学模型的思想：

（1）人口数量与时间（年份）的变化关系问题；

（2）自由落体下落的距离与下落时间的变化关系问题；

（3）某市一天的气温与时间的变化关系问题

3.分析、归纳以上三个实例，它们有什么共同点。

4.引导学生应用集合与对应的语言描述各个实例中两个变量间的依赖关系；

5.根据初中所学函数的概念，判断各个实例中的两个变量间的关系是否是函数关系？如何用集合的语言来描述？

（二）探求新知

1.函数的有关概念

（1）函数的概念：

设A、B是非空的数集，如果按照某个确定的对应关系f，使对于集合A中的任意一个

数x，在集合B中都有唯一的元素y和它对应，那么就称f：A→B为从集合A到集合B的一个函数（function）．记作： y=f(x)，x∈A．

其中，x叫做自变量，x的取值范围A叫做函数的定义域（domain）；与x的值相对应的y值叫做函数值，函数值的集合{f(x)| x∈A }叫做函数的值域（range）．

强调：①任意性；②唯一性。

思考：课本例1 ，对照定义说明理由。

注意：（1）① “y=f(x)”是函数符号，可以用任意的字母表示，如“y=g(x)”；②函数符号“y=f(x)”中的f(x)表示与x对应的函数值，一个数，而不是f乘x．

（2）初中学过哪些函数？它们的定义域、值域、对应法则分别是什么？

①一次函数：y=ax+b      (a≠0)；

②二次函数：y=ax2+bx+c   (a≠0)；

③反比例函数：y=k/x     (k≠0)

（3）函数三要素：

①由定义，构成函数需要几个要素？

②如果一个函数的定义域、对应法则确定，则其值域是否确定？

③如果定义域、值域确定，函数是否确定？为什么？试举例说明。

例：y=x,x∈R；y=-x,x∈R

④由此，两个函数相同的条件是什么？

⑤思考：函数y=f(x)，x∈A与函数s=f(t)，t∈A是同一函数吗？

        函y=x与y=x2/x是同一函数吗？

2.函数的定义域

（1）如果函数对应法则可以用解析式表示出来，那么要确定这个函数，还必须给出定义域。

（2）如果给出了解析式，但未给出定义域，那么我们就认为其定义域就是使其解析式有意义的x的取值集合。

（3）引导学生小结几类函数的定义域：

①如果f(x)是整式，那么函数的定义域是实数集R .

②如果f(x)是分式，那么函数的定义域是使分母不等于零的实数的集合 .

③如果f(x)是二次根式，那么函数的定义域是使根号内的式子大于或等于零的实数集合.

④如果f(x)是由几个部分的数学式子构成的，那么函数定义域是使各部分式子都有意义的实数集合.（即求各集合的交集）

⑤满足实际问题有意义.

3.函数的解析式

⑴函数“y=f(x)”表示y是x的函数,可简记为f(x)，这里“f”即对应法则；

⑵“f”是一个记号，在不同的函数中具有不同的意义；

⑶如果在同一问题中涉及多个函数，为了区别，也常用g(x)、h(x)、φ(x)、F(x)等等来表示；

⑷当自变量x在定义域内取某一确定的值a时，对应的函数值用f(a)来表示，如：f(x)=2x+1，则f(a)=2a+1，f(1)=3．

4.函数的值域

例：求下列函数的值域

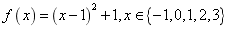⑴ ； ⑵。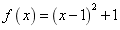

由此，进一步强调函数值域的意义。

【推荐资料】

扫描二维码，关注微信：安徽敏试教育

回复【面试真题】，查看更多安徽教资面试真题内容