教案是课堂教学的蓝图，是教师对一节课的整体设想。创造性的教学设计，严谨、科学的教学策略将有效提高课堂教学效率，让学生们获得最好的学习效果。以下为安徽敏试教育小编为您整理的教案：小学数学教案《集合间的基本关系》。安徽教师资格网为您提供精彩的教案示范，更多面试资讯欢迎关注敏试教育。

【活动方案】

一、教学目标

（一）知识与能力

1.理解子集、真子集、空集的概念；

2.能使用VENN图表达集合间的关系，体会直观图示对理解抽象概念的作用。

（二）过程与方法

让学生通过类比实数间的关系及身边实例，发现集合间的基本关系。

（三）情感态度与价值观

1.树立数形结合的思想，感受符号、图形所带来的魅力，激发学生学习的兴趣；

2.体会类比对发现新结论的作用，养成良好的思维习惯及数学品质。

二、教学重难点

（一）教学重点

集合间基本关系

（二）教学难点

属于关系与包含关系的区别

三、教学方法

引导学生自主探究，合作学习，在教学中引导类比身边实例，来研究集合间的关系，降低了学生学习的难度，同时也激发了学生学习的兴趣，充分体现了以学生为本的教学思想。

四、教学过程

（一）创设情景，揭示课题

问题1：实数有相等、大小关系，如5=5，5＜7，5＞3等，类比实数之间的关系，你会想到集合之间有什么关系呢？

【师生活动】教师不急于做出判断，而是引导学生类比实数间的关系，引出学习内容。

【设计意图】通过类比实数间的关系引出集合间的关系，符合学生的认知规律，可以调动学生探索问题的积极性，加深学生前后知识的联系。

（二）合作交流，探究新知

问题2：观察下面几个例子，你能发现两个集合间的关系吗？ 

（1）A={1，2，3}，B={1，2，3，4，5}；

（2）设A为光明中学高一（2）班全体女生组成的集合，B为这个班全体学生组成的集合；

（3）设A={x|x是两条边相等的三角形}，B={x|x是等腰三角形}。

结论：

1.一般地，对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，我们就说这两集合有包含关系，称集合A为集合B 的子集。

符号表示：AB（BA）

读作：A含于B或B包含A

2.如果两个集合所含的元素完全相同，那么我们称这两个集合相等。

即：若AB，且BA，则A=B。

为了直观地表示集合间的关系，我们常用平面上封闭曲线的内部代表集合，这种图称为Venn图。

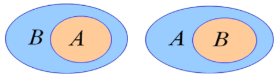
3.如果集合AB，但存在元素xB, 且xA，我们称集合A是集合B的真子集。

符号表示：AB

4.不含有任何元素的集合叫做空集，记为，并规定空集是任何集合的子集。

【师生活动】教师引导学生类比表示集合间关系的符号与表示两个实数大小关系的等号，找出类似之处，强化学生对符号所表示意义的理解。学生充分讨论和交流，发现集合所含元素范围存在各种关系，从而类比得出集合间的关系。

【设计意图】通过具体实例，让学生先观察，后得出结论，培养学生观察、分析、归纳的能力，同时也遵循知识的循序渐进原则。

（三）巩固深化，思维拓展

问题3：包含关系AB与属于关系aA有什么区别？

结论：前者是集合之间的关系，后者是元素与集合间的关系。

问题4：经过以上集合间基本关系的学习，你有什么发现？

结论：

1.任何一个集合都是它本身的子集，即AA。

2.对于集合A，B，C，如果AB，BC，那么AC。

（四）练习反馈，培养能力

用适当的符号填空

1.a___________{a，b，c} 

2.{0，1}___________N 

3.{2，1}___________{X|X2-3X+2=0}

（五）归纳整理，强化认知 

1.请学生回顾本节课所学过的知识内容与所涉及到的主要数学思想方法。

2.在本节课的学习过程中，还有哪些不太明白的地方，向老师提出。

五、教学评价

本节课的知识内容不是很复杂，但有很多方法和思维习惯需要学生了解。学生学习多只注重知识的学习，容易忽略方法和思维习惯学习，在教学中应引起重视。

【推荐资料】

扫描二维码，关注微信：安徽敏试教育

回复【面试真题】，查看更多安徽教资面试真题内容